Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer 论文研读

论文链接：https://arxiv.org/abs/1701.06538

参考链接：https://zhuanlan.zhihu.com/p/542465517

Abstract

The capacity of a neural network to absorb information is limited by its number of parameters. Conditional computation, where parts of the network are active on a per-example basis, has been proposed in theory as a way of dramatically increas-ing model capacity without a proportional increase in computation. In practice, however, there are significant algorithmic and performance challenges. In this work, we address these challenges and finally realize the promise of conditional computation, achieving greater than 1000x improvements in model capacity with only minor losses in computational efficiency on modern GPU clusters. We in-troduce a Sparsely-Gated Mixture-of-Experts layer(MoE), consisting of up to thousands of feed-forward sub-networks. A trainable gating network determines a sparse combination of these experts to use for each example. We apply the MoE to the tasks of language modeling and machine translation, where model capacity is critical for absorbing the vast quantities of knowledge available in the training corpora. We present model architectures in which a MoE with up to 137 billion parameters is applied convolutionally between stacked LSTM layers. On large language modeling and machine translation benchmarks, these models achieve significantly better results than state-of-the-art at lower computational cost.

神经网络吸收信息的能力受限于其参数数量。条件计算（conditional computation）是一种理论上提出的方法，通过在每个样本基础上激活网络的一部分，从而在不显著增加计算量的情况下大幅提升模型容量。然而，在实践中，这一方法面临显著的算法和性能挑战。在本研究中，我们解决了这些挑战，最终实现了条件计算的潜力，在现代GPU集群上实现了超过1000倍的模型容量提升，同时仅带来轻微的计算效率损失。我们引入了一种稀疏门控的专家混合层（Sparsely-Gated Mixture-of-Experts, MoE），该层包含多达数千个前馈子网络。一个可训练的门控网络为每个样本确定这些专家的稀疏组合。我们将MoE应用于语言建模和机器翻译任务，在这些任务中，模型容量对于吸收训练语料库中大量知识至关重要。我们提出了一种模型架构，其中包含多达1370亿参数的MoE被卷积地应用于堆叠的LSTM层之间。在大型语言建模和机器翻译基准测试中，这些模型以较低的计算成本取得了显著优于当前最先进技术的结果。

---

文章声称首次解决了先前条件计算面临的所有挑战，仅以微小的计算效率损失换取了超过1000倍的模型容量提升，并显著提高了公共语言建模和翻译数据集上的SOTA。

The Approach：THE SPARSELY-GATED MIXTURE-OF-EXPERTS LAYER

作者实现条件计算的方法是 引入一种新型的通用神经网络组件：稀疏门控专家混合层（Sparsely-Gated Mixture-of-Experts Layer, MoE）。MoE 由若干专家组成，每个专家是一个简单的前馈神经网络，同时包含一个可训练的门控网络，用于为每个输入选择专家的稀疏组合（见下图），网络的所有部分通过反向传播联合训练。

尽管所引入的技术是通用的，但在本文中，作者主要关注了语言建模和机器翻译任务，这些任务已知能够从超大规模模型中受益。具体而言，我们在堆叠的 LSTM 层（Hochreiter & Schmidhuber, 1997）之间卷积地应用 MoE，如下图所示。MoE 在文本的每个位置被调用一次，每个位置可能选择不同的专家组合，不同的专家往往会基于句法和语义高度专业化。另外，本文作者的工作建立在将 MoEs 作为通用神经网络组件的基础上

图1

The Structure of the MoE Layer

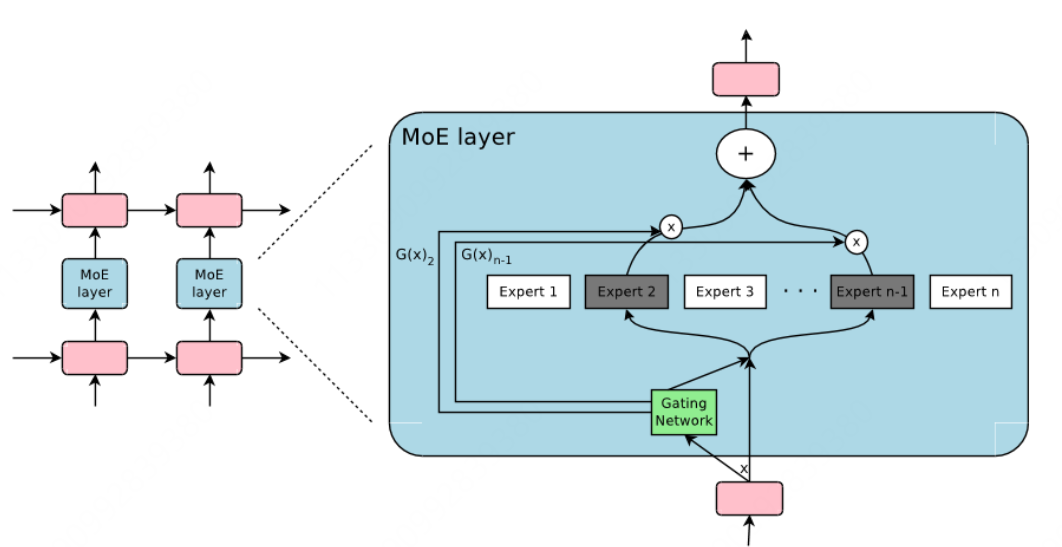
混合专家（MoE）层由一组 $n$ 个”专家网络” $E_1,\cdots,E_n$ 和一个输出为稀疏 $n$ 维向量的”门控网络” $G$ 组成。图 1 （上图）展示了MoE模块的概览。专家本身是神经网络，每个专家都有其自己的参数。虽然原则上我们只要求专家接受相同大小的输入并产生相同大小的输出，但在本文的初步研究中，我们将自己限制在模型是具有相同架构但参数不同（separate parameters）的前馈网络的情况。

让我们用 $G(x)$ 和 $E_i(x)$ 分别表示给定输入 $x$ 时门控网络的输出和第 $i$ 个专家网络的输出。MoE模块的输出 $y$ 可以写作：

$$y = \sum_{i=1}^n G(x)_iE_i(x) \tag{1}$$

基于 $G(x)$ 输出的稀疏性，我们可以节省计算量。当 $G(x)_i = 0$ 时，我们不需要计算 $E_i(x)$。在我们的实验中，我们有多达数千个专家，但对每个样例只需要评估其中少数几个。

如果专家数量非常大，我们可以通过使用两级层次化 MoE（a two-level hierarchical MoE）来减少分支因子。在一个层次化 MoE 中，主门控网络选择 “专家” 的稀疏加权组合，每个专家本身都是具有自己门控网络的次级混合专家。在下文中主要关注普通的 MoE，作者在论文的附录B中提供了关于层次化 MoE 的更多细节。

我们的实现与其他条件计算模型相关，具有简单权重矩阵作为专家的 MoE 类似于(Cho & Bengio, 2014)中提出的参数化权重矩阵。具有一个隐藏层的专家的 MoE 类似于(Bengio et al., 2015)中描述的分块式 dropout，其中 dropout 层被夹在完全激活的层之间。

Gating Network

1. Softmax Gating：

一个简单的非稀疏的门控函数是，将输入与一个可训练的权重矩阵相乘，然后对其应用 Softmax：

$$G_{\sigma} = Softmax(x \cdot W_g) \tag{2}$$

1. Noisy Top-K Gating：

我们在Softmax门控网络中增加两个组件（components）：稀疏性和噪声（sparsity and noise），在应用 softmax 函数之前，我们添加可调高斯噪声（tunable Gaussian noise），然后只保留前k个值，并将其余值设置为负无穷（这会导致相应的门控值等于零），其稀疏性有助于节省计算。虽然这种形式的稀疏性会在门控函数输出中产生一些理论上令人担忧的不连续点，但在实践中尚未观察到这是一个问题。每个组件中的噪声数量由第二个可训练的权重矩阵 $W_{noise}$ 控制。

$$G(x) = Softmax(KeepTopK(H(x),~k)) \tag{3}$$ $$H(x)_i = (x \cdot W_{g})_i + StandardNormal() \cdot Softplus((x \cdot W_{noise})_i) \tag{4}$$ $$KeepTopK(v,~k)_i = \begin{cases} v_i & \text{if }v_i \text{ is in the top } k \text{ elements of } v . \\ -\infty & \text{otherwise.} \end{cases} \tag{5}$$

BALANCING EXPERT UTILIZATION

作者在实验中发现，门控网络倾向于收敛到一种状态：其总是为少数几个专家分配大的权重。这种不平衡是自我强化的（self-reinforcing），因为受青睐的专家会训练地更快，因而也被门控网络选择地更多。

作者采用了一种软约束方法，其将专家相对于一批训练样本的重要性定义为该专家在这批样本上门控值的批次总和，并定义了一个额外的损失项 $L{\text{importance}}$，并将其添加到模型的总体损失函数中。该损失等于重要性值集合的变异系数的平方，再乘以一个手动调整的缩放因子 $w{\text{importance}}$。这一额外的损失项鼓励所有专家具有同等的重要性。

$$Importance(X) = \sum_{x \in X} G(x) \tag{6}$$ $$L_{importance}(X) = w_{importance} \cdot CV(Importance(X))^2 \tag{7}$$

---

与1991年的 Adaptive-Mixtures-of-Local-Experts 中（具体可见：Adaptive Mixtures of Local Experts 论文研读 | Relativity suis’s Blog）做的工作对比：这里的 MoE 主要有两个区别：

1. 稀疏门控：不是所有专家都会起作用，而是极少数的专家会被使用来进行推理，这种稀疏性，也使得我们可以使用海量的专家来把模型容量做的超级大。
2. token-level：前者的工作，是 sample-level 的，即不同的样本，使用不同的专家，但是这篇则是 token-level 的，一个句子中不同的 token 使用不同的专家，如论文中说：

The MoE is called once for each position in the text, selecting a potentially different combination of experts at each position.

这篇文章的工作是在 RNN 中添加了 MoE 层，如上图（图1）所示，即每个 token 对应的位置（position）都会有一个 MoE 层，每个 MoE 层包含了一堆的专家（Experts, $\text{Expert}_{1 \cdots n}$ ），每个专家都是一个小型的 FFN，Gating Network 则会根据当前 position 的输入，选择少数几个专家来进行计算。

一些问题

问题1：如何控制门控网络输出的为一个稀疏的权重向量，具体来说Noisy Top-K门控是如何实现这一点的？
问题2：可调的高斯噪声是什么，为什么添加它可以增加模型的鲁棒性？
问题3：在平衡专家利用中引入的额外损失项为什么可以解决专家利用不平衡的问题？

问题1：如何控制门控网络输出为一个稀疏的权重向量，具体来说 Noisy Top-K 门控是如何实现这一点的？

理解稀疏权重向量

在混合专家模型（Mixture-of-Experts, MoE）中，门控网络的任务是为每个输入选择一部分专家进行计算。稀疏权重向量意味着在所有专家中，只有少数几个（如前K个）被激活并用于当前输入，而其余的专家权重为零，从而节省计算资源。

Noisy Top-K 门控的实现步骤

Noisy Top-K门控机制通过以下步骤实现稀疏权重向量：

1. 计算初始门控得分（Gating Scores）：

   对于给定输入 $x$，门控网络首先计算每个专家的初始得分：

   $$S_i = x \cdot W_g$$

   其中，$W_g$ 是门控网络的权重矩阵，$S_i$ 是第 $i$ 个专家的得分。

2. 添加可调的高斯噪声（Add Tunable Gaussian Noise）：

   为了增加选择的多样性和鲁棒性，向每个专家的得分中添加可调的高斯噪声：

   $$H_i = S_i + \text{StandardNormal()} \times \text{Softplus}(x \cdot W_{noise})$$

   其中：

   • $\text{StandardNormal()}$ 表示从标准正态分布（均值为0，方差为1）中采样的随机噪声。
   • $W_{noise}$ 是另一个可训练的权重矩阵，用于控制噪声的幅度。
   • $\text{Softplus}(\cdot)$ 是一种平滑的激活函数，确保噪声幅度为正。

3. 选择Top-K得分（Keep Top-K）：

   从加噪后的得分 $H$ 中选择前K个最高的值，其余的设置为负无穷：

   $$\text{KeepTopK}(H, K)_i = \begin{cases} H_i & \text{如果 } H_i \text{ 是前 } K \text{ 个最大值之一} \\ -\infty & \text{否则} \end{cases}$$

   这样，只有前K个专家的得分保持有效，其他专家的得分变为负无穷，经过Softmax后对应的权重为零。

4. 应用Softmax函数（Apply Softmax）：

   对保留后的得分应用 Softmax 函数，得到稀疏的权重向量：

   $$G(x)_i = \text{Softmax}(\text{KeepTopK}(H, K)_i)$$

   由于大多数值为负无穷，Softmax 会将这些值对应的权重计算为零，仅前 K 个专家拥有非零权重。

   问题2：可调的高斯噪声是什么，为什么添加它可以增加模型的鲁棒性？

   可调的高斯噪声的定义

可调的高斯噪声是指具有可调参数（如均值和方差）的高斯（正态）分布噪声。在 Noisy Top-K 门控中，这种噪声被添加到门控得分中，以实现更灵活和鲁棒的专家选择。
具体来说，论文中使用的噪声项定义为：

$$\text{Noise}_i = \text{StandardNormal()} \times \text{Softplus}(x \cdot W_{noise})$$

其中：

• $\text{StandardNormal()}$ 是从标准正态分布（均值为0，方差为1）中采样的随机噪声。
• $W_{noise}$ 是一个可训练的权重矩阵，用于控制噪声的幅度。
• $\text{Softplus}(\cdot)$ 确保噪声幅度为正。

  为什么添加高斯噪声可以增加模型的鲁棒性？

  增加模型鲁棒性的原因主要包括以下几个方面：

1. 促进专家的多样性（Diversity of Experts）：

   添加噪声打破了门控网络对专家选择的确定性，使得在不同训练迭代或不同输入下，专家的选择更加多样化。这有助于避免模型过度依赖某些特定的专家，从而使得各个专家能够学习到更多不同的特征和表示。

2. 防止过拟合（Preventing Overfitting）：

   如果门控网络总是选择同样的专家，某些专家可能会过度训练，而其他专家则几乎不被训练。噪声的引入鼓励门控网络探索不同的专家组合，避免了特定专家的过拟合。

3. 提高模型的泛化能力（Improving Generalization）：

   通过引入噪声，模型在面对未见过的数据时，能够更好地适应不同的专家组合，提升了整体的泛化能力。这意味着模型在处理新样本时，能够更灵活地调用不同的专家，从而更准确地进行预测或翻译。

4. 增强训练的稳定性（Enhancing Training Stability）：

   噪声的引入可以平滑门控网络的决策边界，使得模型在训练过程中更不容易陷入局部最优解。这样，模型能够更全面地探索专家空间，找到更优的参数配置。

   具体机制解释

   在 Noisy Top-K 门控中，噪声的引入是有目的的：

• 探索性选择（Exploratory Selection）：

  噪声打破了门控网络对专家得分的严格排序，允许一些得分较低但仍具潜力的专家被选中。这种探索性选择有助于发现更多有用的专家，提高整体模型的表现。

• 平滑专家的利用（Smoothing Expert Utilization）：

  通过引入噪声，门控网络不会总是选择同样的专家，这有助于平衡各个专家的使用频率，避免某些专家被频繁使用而其他专家被忽略。

  问题3：在平衡专家利用中引入的额外损失项为什么可以解决专家利用不平衡的问题？

  专家利用不平衡的问题

在 MoE 模型中，由于门控网络的决策，某些专家可能会被频繁选择，而其他专家则很少或根本不被使用。这种专家利用不平衡会导致：

1. 有限的模型容量：尽管模型总体参数量大，但实际只有少数专家在工作，限制了模型的表达能力。
2. 训练不充分：被频繁选择的专家会得到更多的训练，而未被选择的专家几乎不被训练，导致其性能不足。
3. 资源浪费：部分专家被闲置，浪费了模型的潜在资源和计算能力。

引入额外损失项的目的

为了 平衡专家的利用率，论文提出在损失函数中引入一个额外的损失项 $L_{\text{importance}}$。这个损失项旨在鼓励所有专家被均衡地使用，从而解决专家利用不平衡的问题。

具体实现步骤

1. 定义专家的重要性（Importance）：

   对于一个批次的训练样本 $X$，定义每个专家的重要性为该专家在这批样本中被选择的总和：

   $$\text{Importance}(X) = \sum_{x \in X} G(x)$$

   其中，$G(x)$ 是输入 $x$ 的门控权重向量，表示各专家的选择权重。

2. 计算变异系数（Coefficient of Variation, CV）：

   变异系数是标准差与均值的比值，用于衡量数据的相对变异程度：

   $$\text{CV}(\text{Importance}(X)) = \frac{\text{Std}(\text{Importance}(X))}{\text{Mean}(\text{Importance}(X))}$$

   高 CV 值表示专家利用的不平衡性较大，低 CV 值表示专家利用较为均衡。

3. 定义额外损失项 $L_{\text{importance}}$：

   为了最小化专家利用的变异性，定义损失项为变异系数的平方，再乘以一个缩放因子 $w_{\text{importance}}$：

   $$L_{\text{importance}}(X) = w_{\text{importance}} \cdot \text{CV}(\text{Importance}(X))^2$$

   这个损失项的目标是 最小化专家利用的变异系数，即鼓励专家利用的均衡性。

4. 总体损失函数：

   将额外的损失项加入到模型的总体损失函数中：

   $$L_{\text{total}} = L_{\text{task}} + L_{\text{importance}}$$

   其中，$L_{\text{task}}$ 是原始的任务损失（如语言建模的交叉熵损失）。

   为什么额外损失项可以解决专家利用不平衡的问题？

   引入 $L_{\text{importance}}$ 的原因和作用可以从以下几个方面理解：

5. 惩罚不平衡性：

   $L_{\text{importance}}$ 随着专家利用的不平衡性增加而增加。这迫使模型在训练过程中不仅要优化任务损失，还要尽量保持各专家的利用率一致。

6. 鼓励均衡选择：

   通过最小化变异系数，模型被鼓励在选择专家时更加均衡，避免过度依赖某些专家。这有助于所有专家都有机会参与到训练和推理中，充分发挥各自的潜力。

7. 防止自我强化（Self-Reinforcement）：

   如果没有平衡机制，门控网络可能会倾向于选择表现最好的专家，从而使这些专家进一步优化并被更多选择，形成自我强化的循环。而 $L_{\text{importance}}$ 破坏了这种循环，迫使模型在选择专家时考虑整体的利用平衡。