Adaptive Mixtures of Local Experts 论文研读

论文链接：https://people.engr.tamu.edu/rgutier/web_courses/cpsc636_s10/jacobs1991moe.pdf

参考链接：https://zhuanlan.zhihu.com/p/423447025

Abstract

We present a new supervised learning procedure for systems composed of many separate networks, each of which learns to handle a subset of the complete set of training cases. The new procedure can be viewed either as a modular version of a multilayer supervised network, or as an associative version of competitive learning. It therefore provides a new link between these two apparently different approaches. We demonstrate that the learning procedure divides up a vowel discrimi-nation task into appropriate subtasks, each of which can be solved by a very simple expert network.

我们提出了一种新的监督学习过程，适用于由多个独立网络组成的系统，每个网络学习处理完整训练案例集中的一部分（一个子集）。这一新过程既可以视为多层监督网络的模块化版本，也可以看作是竞争学习的关联版本。因此，它在两种看似不同的方法之间建立了新的联系。我们证明了该学习过程能够将元音辨别任务分解为适当的子任务，每个子任务都可以由一个非常简单的专家网络解决。

Making Associative Learning Competitive

对于传统的学习模型来说，训练的主要目的是使模型最终能够在不同的场景下执行多种任务，但这种训练方式也使得模型在对相应场景进行权重更新的同时，也会影响到模型对其它场景的权重。文章中提到：

若采用反向传播算法训练一个单一的多层网络，使其在不同场合执行不同的子任务，通常会产生强烈的干扰效应（interference effects），导致学习速度缓慢和泛化能力差（lead to slow learning and poor generalization）。

因此，如果我们预先知道一组训练案例可以自然地划分为对应于不同子任务的子集，那么干扰效应就可以通过使用一个由多个不同的 “专家” 网络（Expert networks）和一个门控网络（gating network）组成的系统被减弱，其中门控网络决定每个训练案例应该使用哪个专家网络。

接着作者描述了前人研究的两种系统：

①Hampshire 和 Waibel（1989年）描述了一种这样的系统，它可以在训练前已知子任务划分的情况下使用；

②Jacobs 等人（1990年）描述了一种相关的系统，该系统学习如何将案例分配给专家，这种系统的核心思想是，门控网络将新案例分配给一个或少数几个专家，如果输出不正确，则权重的调整仅限于这些被分配过案例的专家（以及门控网络）。因此，不会干扰到专门处理完全不同案例的其他专家的权重。从这个意义上说，专家是局部的，因为一个专家的权重与其他专家的权重是解耦的。此外，专家通常在另一种意义上也是局部的，即每个专家只被分配到可能的输入向量空间的一个小的局部区域。

但是，Hampshire 和 Waibel 以及 Jacobs 等人所使用的误差函数并未促进局部化。他们假设整个系统的最终输出是局部专家输出的线性组合（linear combination of the outputs of the local experts），而门控网络则决定了每个局部输出在线性组合中的比例。所以对于一个案例 $c$ 的误差函数为：

$E^{c}\,=\,\|{\bf d}^{c}-\sum_{i}{p}_{i}^{c}{\bf o}_{i}^{c}\,\|^{2} \tag{1.1}$

其中，${\bf o}{i}^{c}$ 是专家 $i$ 在案例 $c$ 中的输出向量，$p{i}^{c}$ 是专家 $i$ 对（线性）组合输出向量的贡献比例，${\bf d}^c$ 是案例 $c$ 中期望的输出向量。

上述误差的度量是将期望输出与局部专家输出的混合结果进行比较，因此，为了最小化误差，每个局部专家必须使他们的输出抵消由所有其他专家的联合效应留下的残差。当一个专家的权重发生变化时，残差也会变化，因此所有其他局部专家的误差导数也会变化。这种专家之间的强耦合使它们能够很好地合作，但往往会导致每个案例使用多个专家的解决方案。可以通过在目标函数中添加惩罚项来鼓励竞争，以鼓励只有一个专家活跃的解决方案（Jacobs等，1990年），但更简单的补救方法是重新定义误差函数，以鼓励局部专家竞争而不是合作。

而作者的工作不是将各个专家的输出进行线性组合，而是设想门控网络在每次使用时随机决定使用哪个单一专家，误差则是期望输出向量与实际输出向量之间差异平方的期望值：

$E^{c}=\langle\|\mathbf{d}^{c}-\mathbf{o}_{i}^{c}\|^{2}\rangle=\sum_{i}p_{ i}^{c}\|\mathbf{d}^{c}-\mathbf{o}_{i}^{c}\|^{2} \tag{1.2}$

在这个新的误差函数中，每个专家需要生成整个输出向量，而不仅仅是残差。因此，给定训练案例中局部专家的目标不会直接受到其他局部专家权重的影响。仍然存在一些间接耦合，因为如果其他专家改变了其权重，可能会导致门控网络改变分配给专家的责任，但至少这些责任的变化不会改变局部专家在给定训练案例中感知到的误差符号。如果门控网络和局部专家都是通过梯度下降法在这个新的误差函数中进行训练，系统往往会为每个训练案例分配一个专家。每当一个专家的误差小于所有专家误差的加权平均值（使用门控网络的输出来决定如何加权每个专家的误差）时，它对该案例的责任将会增加；而当它的表现比加权平均值差时，其责任将会减少。

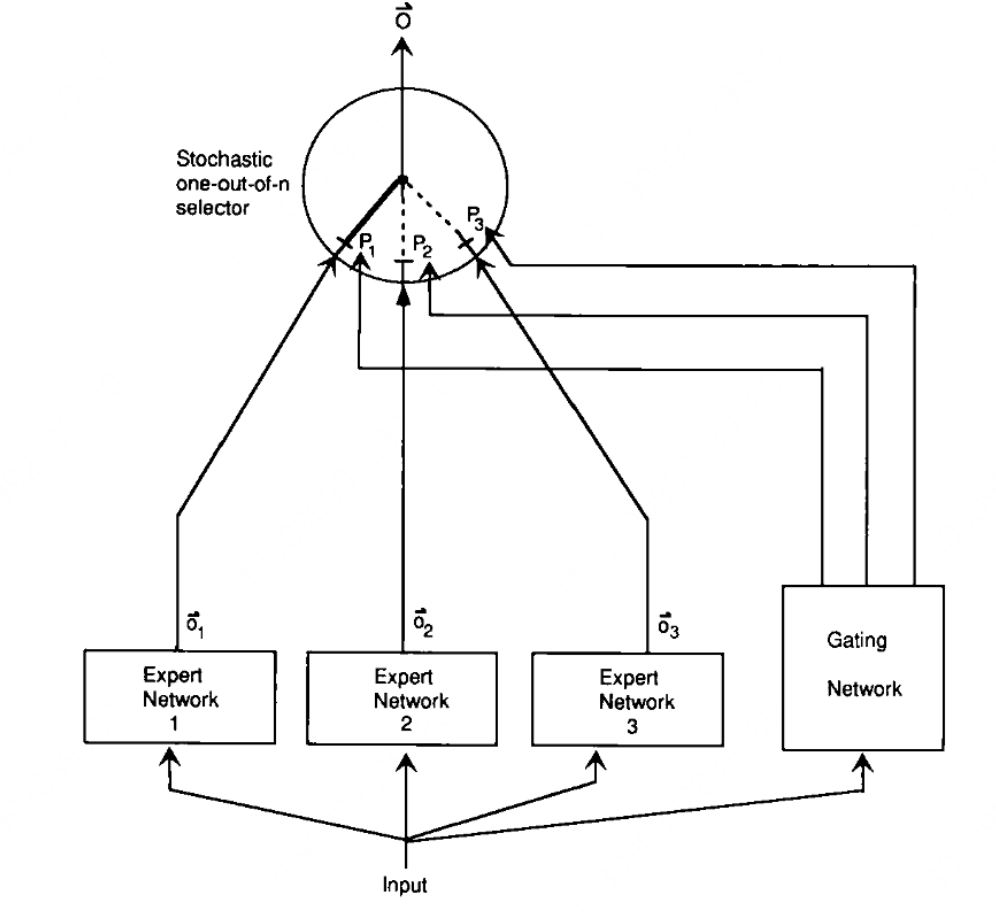
moe91-1

图1：一个由专家网络和门控网络组成的系统。每个专家都是一个前馈网络，所有专家接收相同的输入并具有相同数量的输出。门控网络也是前馈的，通常接收与专家网络相同的输入。它的输出经过归一化处理，即 $pj = \frac{\exp(x_j)}{\sum{i} \exp(x_i)}$，其中 $x_j$ 是门控网络输出单元 $j$ 接收到的总加权输入。选择器就像一个多输入、单输出的随机开关；开关选择专家 $j$ 的输出的概率为 $p_j$。

上述新的误差函数在实践中有效，但在下面的模拟中作者使用了另一个误差函数，效果更好：

$E^{c} = -\log\sum_{i} p_{i}^{c}e^{-\frac{1}{2}||\mathbf{d}^{c}- \mathbf{o}_{i}^{c}||^{2}} \tag{1.3}$

以上定义的误差是在下一节末尾描述的高斯混合模型下生成期望输出向量的负对数概率，为了理解为什么这个误差函数效果更好，比较两个误差函数对专家输出的导数是有帮助的。由方程 1.2 可以得到：

$\frac{\partial{E^c}}{\partial{\mathbf{o}_i^c}} = -2p_i^c({\bf d}^c-\mathbf{o}_i^c) \tag{1.4}$

由方程 1.3：

$\frac{\partial E^c}{\partial \mathbf{o}_i^c} = -\left[\frac{p_i^c e^{-\frac{1}{2}\|\mathbf{d}^c-\mathbf{o}_i^c\|^2}}{\sum_j p_j^c e^{-\frac{1}{2}\|\mathbf{d}^c-\mathbf{o}_j^c\|^2}}\right](\mathbf{d}^c - \mathbf{o}_i^c) \tag{1.5}$

①在方程 1.4 中，项 $p_i^c$ 用于为专家 $i$ 的导数加权；

②在方程 1.5 中，我们使用了一个权重项，该项考虑了专家 $i$ 相对于其他专家的表现程度。这是一个更有用的衡量专家 $i$ 对训练案例 $c$ 的相关性的指标，特别是在训练的早期阶段。例如，假设门控网络最初给所有专家赋予相等的权重，且对所有专家来说 $||{\bf d}^c - {\bf o}_i^c|| > 1$。方程 1.4 将最慢地调整最佳拟合专家，而方程 1.5 将最快地调整它。

Making Competitive Learning Associative

自然地，我们会认为竞争网络训练的“数据”向量类似于关联网络的输入向量，这些输入向量被映射到输出向量。在使用竞争学习作为关联网络预处理阶段的模型中，这种对应关系被假定存在（Moody 和 Darken 1989）。然而，另一种截然不同的观点认为，竞争学习中的数据向量对应于关联网络的输出向量。在这种情况下，竞争网络可以被视为一个无输入的随机输出向量生成器，而竞争学习则可以被视为一种使网络生成与“数据”向量分布相匹配的输出向量分布的过程。每个竞争隐藏单元的权重向量代表了一个多维高斯分布的均值，输出向量的生成过程首先是通过选择一个隐藏单元，然后从由该隐藏单元的权重向量确定的高斯分布中选择一个输出向量。生成任意特定输出向量 ${\bf o}^c$ 的对数概率：

$\log P^c = \log \sum_i p_{i}ke^{-\frac{1}{2}\|\boldsymbol{\mu}_i-\mathbf{o}^c\|^2}$

其中 $i$ 是隐藏单元的索引，$\boldsymbol{\mu}_i$ 是隐藏单元的”权重”向量，$k$ 是归一化常数，$p_i$ 是选择隐藏单元 $i$ 的概率，因此 $p_i$ 之和受约束等于1。在统计文献中（McLachlan and Basford 1988），$p_i$ 被称为”混合比例”。

“软”竞争学习通过修改权重（以及方差和混合比例）来增加生成训练集中输出向量的概率的乘积（即似然度）(Nowlan 1990a)。”硬”竞争学习是软竞争学习的一个简单近似，它忽略了数据向量可能由几个不同隐藏单元生成的可能性。相反，我们假设数据向量必须由具有最接近权重向量的隐藏单元生成，因此只需要修改这个权重向量来增加生成数据向量的概率。

如果我们将竞争网络视为生成输出向量的系统，输入向量可能扮演的角色并不是立即显而易见的。然而，竞争学习可以以与Barto(1985)泛化学习自动机相似的方式进行泛化，即通过添加输入向量并使自动机的行为依赖于输入向量。我们用整个专家网络替换竞争网络中的每个隐藏单元，其输出向量指定了多维高斯分布的均值。因此，均值现在是当前输入向量的函数，并且由活动水平而不是权重来表示。此外，我们使用一个门控网络，它允许专家的混合比例由输入向量决定。这给了我们一个由局部专家组成的竞争系统，其误差函数在等式1.3中定义。我们也可以引入一个机制，允许输入向量动态确定每个专家网络定义的分布的协方差矩阵，但我们还没有尝试过这种可能性。

一些理解

一、背景与动机

在传统的监督学习中，我们常用一个多层神经网络来处理各种任务。然而，当同一个网络需要学习处理多种不同的子任务时，会出现干扰效应（interference effects）：在训练网络以适应一个场景时，不可避免地会影响到它在其他场景下的表现。这种干扰会导致学习速度变慢，泛化能力变差。
问题：如何设计一个系统，使得每个子任务由专门的“专家网络”来处理，从而减少不同任务之间的干扰？
解决思路：引入多个独立的专家网络，每个专家专注于处理一小部分任务或特定的输入模式，再通过一个门控网络决定使用哪个专家。这种架构被称为 “混合专家模型”（Mixture of Experts）。

二、混合专家模型的基本结构

模型主要由两部分组成：

专家网络（Expert Networks）：多个并行的子网络，各自独立处理不同的任务或数据子集。
门控网络（Gating Network）：一个网络，根据输入数据决定哪个专家（或哪些专家）的输出最适合当前任务。
在每次处理一个输入时，门控网络会评估哪个专家最有可能给出正确的结果，并选择相应的专家来生成输出。

三、传统方法的问题与改进方向

传统的误差函数与专家组合

过去的一种常见方法是让整个系统的输出作为各个专家输出的线性组合。形式上，对于某个训练样本 $c$，误差函数定义为：

$E^{c} = \Big\| \mathbf{d}^{c} - \sum_{i} p_i^c \mathbf{o}_i^c \Big\|^2$

$\mathbf{d}^c$：期望的输出向量
$\mathbf{o}_i^c$：专家 $i$ 对应样本 $c$ 的输出
$p_i^c$：门控网络给予专家 $i$ 的权重（对应其在输出组合中的贡献比例）
问题：这种设置下，各个专家需要协同工作来共同逼近期望输出。这意味着：
当一个专家调整权重时，会影响剩余专家需要补偿的残差，从而间接影响其它专家的工作。
导致多个专家可能都参与到一个样本的处理上，增加了干扰和复杂性。
改进方向：鼓励竞争而非合作
为了解决上述问题，作者提出改变误差函数，使专家之间竞争而非合作。这样，每个训练案例最终倾向于分配给一个最合适的专家，而不是多个专家共同处理。

四、第一种实现思路 —— 使关联学习具有竞争性

核心思想：重新定义误差函数，让门控网络在每次选择时随机决定使用哪个单一的专家，而不是线性组合多个专家的输出。
新的误差函数定义为：

$E^{c} = \sum_{i} p_{i}^{c}\,\|\mathbf{d}^{c}-\mathbf{o}_{i}^{c}\|^{2}$

其中：

仍然保持 $p_i^c$ 代表门控网络选择专家 $i$ 的概率。
这个误差函数表示：对于每个可能的专家 $i$，以其被选择的概率加权，它单独产生的输出与期望输出之间的误差。
效果：
每个专家独立地尝试对整个输出负责，而不只是去补偿其他专家留下的残差。
当某个专家在处理某个样本时表现优于其他专家，它获得的“责任”会增加，从而更多地参与到类似样本的学习中。

为了进一步改进效果，作者提出了一个变体的误差函数：

$E^{c} = -\log\sum_{i} p_{i}^{c}e^{-\frac{1}{2}\|\mathbf{d}^{c}- \mathbf{o}_{i}^{c}\|^{2}}$

此公式的优势在于：

在计算梯度时，会自然地更快地调整表现最佳的专家，而不是平均调整所有专家。
这通过一个softmax风格的权重机制，自动放大那些与期望输出更接近的专家的影响，鼓励更快地专精化。
具体效果：
在训练早期，当所有专家的表现都较差时，新误差函数能更快地找到并调整最有潜力的专家。
这种机制减少了多个专家在同一个任务上的不必要竞争，使得一个专家更快地“专精”于某些数据区域。

五、第二种实现思路 —— 使竞争学习具有联想性

背景：竞争学习通常用于无监督聚类，比如找到数据中的典型模式或中心（如聚类中心）。在传统的竞争学习中，每个隐藏单元代表一个聚类中心，数据点被分配到距离最近的中心。
转换思路：将竞争学习的思想引入到关联（即输入输出映射）的情境中，把竞争网络看作一个生成输出向量的系统，而不仅仅是对输入聚类。

概率模型视角：
- 假设每个隐藏单元对应一个多维高斯分布，均值由该单元的权重向量决定。
- 给定一个输出向量 $\mathbf{o}^c$，其生成概率可以表示为高斯混合模型的形式：
  - $\boldsymbol{\mu}_i$：隐藏单元 $i$ 的权重向量，相当于高斯分布的均值
  - $p_i$：选择隐藏单元 $i$ 的概率，称为混合比例
软硬竞争学习：
- 软竞争学习：根据整个概率分布调整所有单元的权重，使得训练数据的似然度最大化。
- 硬竞争学习：简化处理，只调整对给定数据点贡献最大的那个单元的权重。
关联性引入：
- 将每个竞争学习的隐藏单元替换为一个专家网络，使得该网络的输出（而非固定权重）决定高斯分布的均值。
- 引入门控网络，使得混合比例 $p_i$ 依赖于输入向量，而不再是常数。
- 结果是一个输入-输出映射系统：给定输入后，门控网络决定调用哪个专家网络，而该专家网络生成输出。

意义：

这种设置把传统的竞争学习（无监督）与监督学习结合起来，构建了一个能够根据输入生成适当输出的系统。
专家网络不仅仅是简单的固定聚类中心，而是可以根据输入动态调整输出，提供更灵活的映射能力。

一些疑问

问题1：在传统方法上，为什么当一个专家调整权重时，会影响剩余专家需要补偿的残差，这里“需要补偿的残差”的什么意思？
问题2：为什么通过对新误差函数与其变体的误差函数的导数进行比较，就能得出其变体效果更好，如何进行比较的？
问题3：这种网络是如何进行训练的？
问题4：门控网络如何决定调用哪个专家网络？

问题1：在传统方法上，为什么当一个专家调整权重时，会影响剩余专家需要补偿的残差，这里“需要补偿的残差”的什么意思？

理解传统方法中的“残差补偿”
背景回顾：
在传统的混合专家模型中，系统的最终输出是各个专家网络输出的线性组合。具体来说，对于一个训练样本 $c$，系统的输出是：

$\mathbf{O}^c = \sum_{i} p_i^c \mathbf{o}_i^c$

其中：

$\mathbf{o}_i^c$ 是专家 $i$ 对样本 $c$ 的输出。
$p_i^c$ 是门控网络为专家 $i$ 分配的权重（概率）。

误差函数：
误差定义为期望输出 $\mathbf{d}^c$ 与系统输出 $\mathbf{O}^c$ 之间的差距：

$E^{c} = \| \mathbf{d}^c - \mathbf{O}^c \|^2 = \left\| \mathbf{d}^c - \sum_{i} p_i^c \mathbf{o}_i^c \right\|^2$

残差补偿的含义：

残差（Residual）： 指的是当前系统输出与期望输出之间的差距，即 $\mathbf{d}^c - \mathbf{O}^c$。
补偿残差： 每个专家网络的输出 $\mathbf{o}_i^c$ 都在尝试减小这个残差，使系统输出更接近期望输出。

为何调整一个专家影响其他专家：

线性组合的依赖性： 因为系统输出是所有专家输出的加权和，改变某一个专家的输出 $\mathbf{o}_i^c$ 会直接影响 $\mathbf{O}^c$。
残差的变化： 当某个专家调整了其输出 $\mathbf{o}_i^c$，整个系统的残差 $\mathbf{d}^c - \mathbf{O}^c$ 也会相应变化。
其他专家的响应： 由于残差变化，其他专家需要调整它们的输出以重新补偿新的残差，以维持系统输出的准确性。

举个简单的例子：
假设有两个专家 A 和 B：

系统输出 $\mathbf{O} = p_A \mathbf{o}_A + p_B \mathbf{o}_B$。
初始时，A 和 B 都有一定的输出，系统输出接近期望输出。

如果专家 A 调整了其输出 $\mathbf{o}_A$（例如增加了输出值），那么系统输出 $\mathbf{O}$ 会增加，从而引入一个新的残差（假设期望输出保持不变）。为了减小新的残差，专家 B 需要调整其输出 $\mathbf{o}_B$ 来补偿 A 的变化。这样，A 的调整直接导致了 B 的响应，形成了专家之间的强耦合。

问题2：为什么通过对新误差函数与其变体的误差函数的导数进行比较，就能得出其变体效果更好，如何进行比较的？

理解误差函数变体及其梯度对训练效果的影响
原始误差函数 vs. 变体误差函数：

原始误差函数：
$E^{c} = \left\| \mathbf{d}^c - \sum_{i} p_i^c \mathbf{o}_i^c \right\|^2$
变体误差函数：
$E^{c} = -\log\left( \sum_{i} p_i^c e^{-\frac{1}{2} \| \mathbf{d}^c - \mathbf{o}_i^c \|^2} \right)$

为什么比较导数有助于判断效果：

梯度下降法： 在训练神经网络时，我们通常使用梯度下降法来最小化误差函数。梯度（导数）决定了参数更新的方向和幅度。
影响训练过程： 误差函数的梯度影响模型如何调整参数以减少误差。不同的误差函数会导致不同的梯度，从而影响模型的学习速度和收敛效果。

比较导数的具体方式：

计算各自的梯度：
- 原始误差函数的梯度：
  - 解释： 每个专家的输出梯度与其分配的权重 $p_i^c$ 和输出误差 $(\mathbf{d}^c - \mathbf{o}_i^c)$ 成正比。
- 变体误差函数的梯度：
  - 解释： 每个专家的梯度不仅取决于其分配的权重和输出误差，还受到一个额外的归一化因子的调节，这个因子反映了专家相对于其他专家的表现。
分析梯度的影响：
- 原始误差函数： 所有专家都会根据它们的权重和误差调整输出。即使某些专家的表现较差（误差大），它们也会对梯度有贡献，但这种贡献是平均的。
- 变体误差函数： 梯度的贡献被加权，表现较好的专家（误差较小，靠近期望输出）的梯度贡献相对较大，而表现较差的专家的贡献较小。具体来说，变体误差函数的梯度对表现好的专家更敏感，促进这些专家更快地调整以进一步优化输出。
效果上的优势：
- 加速最佳专家的调整： 由于变体误差函数在梯度中对表现好的专家赋予更大的权重，这些专家能够更快地调整和优化，迅速适应特定的子任务或数据模式。
- 鼓励专家间的竞争： 变体误差函数自然地促进了专家之间的竞争，优秀的专家会得到更多的关注和资源，而表现差的专家则会逐渐被淘汰或调整以适应更合适的任务。

问题3：这种网络是如何进行训练的？

理解混合专家模型的训练流程
模型组成：

专家网络（Expert Networks）： 多个独立的子网络，每个负责处理特定的子任务或数据子集。
门控网络（Gating Network）： 一个网络，用于根据输入数据决定使用哪个专家（或哪些专家）。

训练步骤：

初始化：
- 参数初始化： 随机初始化所有专家网络和门控网络的参数（权重和偏置）。
前向传播（Forward Pass）：
- 输入处理： 对于每一个训练样本 $c$：
  - 将输入向量 $\mathbf{x}^c$ 传递给所有专家网络，得到各自的输出 $\mathbf{o}_i^c$。
  - 将输入向量 $\mathbf{x}^c$ 传递给门控网络，得到各专家的选择概率 $p_i^c$（通常通过 Softmax 函数归一化）。
输出组合：
- 系统输出： 计算系统的最终输出 $\mathbf{O}^c = \sum_{i} p_i^c \mathbf{o}_i^c$。
误差计算：
- 原始误差函数：
  $E^{c} = \left\| \mathbf{d}^c - \mathbf{O}^c \right\|^2$
- 变体误差函数：
  $E^{c} = -\log \left( \sum_{i} p_i^c e^{-\frac{1}{2} \| \mathbf{d}^c - \mathbf{o}_i^c \|^2} \right)$
反向传播（Backward Pass）：
- 计算梯度： 根据选定的误差函数，计算所有专家网络和门控网络参数的梯度。
- 更新参数： 使用梯度下降或其变体（如随机梯度下降、Adam 等）更新所有网络的参数：
  $\theta \leftarrow \theta - \eta \frac{\partial E^c}{\partial \theta}$
  其中 $\theta$ 代表所有网络的参数，$\eta$ 是学习率。
重复训练：
- 迭代训练： 对整个训练集进行多次迭代（Epochs），不断优化专家和门控网络的参数，直到误差收敛或达到预设的训练轮数。
  具体细节：
- 专家网络的调整：
  - 在原始误差函数下，所有专家的输出都会影响系统输出，因此所有专家都会根据各自的误差调整参数。
  - 在变体误差函数下，梯度更倾向于那些表现较好的专家，促使这些专家更快地优化其输出。
- 门控网络的调整：
  - 门控网络通过调整 $p_i^c$ 来优化专家的选择，使得系统输出更接近期望输出。
  - 在变体误差函数下，门控网络会逐渐学会更倾向于选择那些能够更好地处理特定输入的专家。

问题4：门控网络如何决定调用哪个专家网络？

理解门控网络的工作机制
门控网络的角色：
门控网络的主要任务是根据输入数据决定使用哪个专家网络来处理当前样本。它充当“调度员”的角色，动态分配任务给最合适的专家。
具体机制：

输入传递：
- 门控网络接收与专家网络相同的输入向量 $\mathbf{x}^c$。
生成概率分布：
- 门控网络输出一组分数 $x_j$（未归一化的权重），每个分数对应一个专家网络。
- 这些分数通过 Softmax 函数转换为概率 $p_j$：
  - Softmax 函数的作用： 将分数转化为一个概率分布，确保所有 $p_j$ 之和为 1。
选择专家：
- 确定性选择（Hard Selection）： 选择具有最高概率 $p_j$ 的专家 $j$ 作为当前样本的处理者。
  - 优点： 简单高效，每次仅使用一个专家，降低计算开销。
  - 缺点： 可能导致门控网络过于偏向某些专家，忽略其他专家的潜力。
- 概率性选择（Soft Selection）： 根据概率分布 $p_j$ 随机选择一个专家 $j$。
  - 优点： 保留多个专家的参与机会，促进更全面的专家训练。
  - 缺点： 可能导致训练不稳定，因为不同专家可能随机被选择。
- 混合策略： 在训练早期使用概率性选择，逐渐转向确定性选择，以平衡探索和利用。
训练期间的专家分配：
- 在训练过程中，门控网络通过误差函数的梯度反馈不断优化其决策，使得更适合处理特定输入的专家获得更高的选择概率。
- 特别是在使用变体误差函数时，门控网络更倾向于选择那些表现更好的专家，从而促进专家的专精化。
推理阶段的专家选择：
- 确定性选择通常用于推理阶段， 以确保高效的计算和稳定的输出。
- 通过选择概率最高的专家，系统能够快速响应并生成准确的输出。

图示说明：

输入向量 x^c
      |
      v
+---------------+
| 门控网络 G     |
+---------------+
      |
      v
p_1, p_2, ..., p_n  (Softmax 概率分布)
      |
      v
选择专家 j（确定性或概率性）
      |
      v
+---------------+
| 专家网络 E_j   |
+---------------+
      |
      v
系统输出 O^c = o_j^c